Řešení problému batohu pomocí tabu prohledávání

Úvod

Tabu prohledávání je jeden ze způsobů jak se vyhnout uváznutí v lokálním minimu.

Při běhu se využívají dva druhy informací - dlouhodobé a krátkodobé. Krátkodobé informace slouží k tomu, aby se prohledávací algoritmus mohl vyhnout opakování několika stejných operací pořád dokola a tím se zacyklil. Dlouhodobé informace můžeme využít při výpočtu hodnotící funkce nebo při restartu algoritmu.

Popis implementace

• Nejlepší nalezený stav
• Počet výskytů předmětu v batohu
• Počet výskytů předmětu mimo batoh
• Počet kroků od posledního zlepšení

• Tabu seznam na vložené/vyjmuté předměty, velikost sqrt(počet předmětů * 2)
• Tabu seznam na hodnoty heuristické funkce, velikost (počet předmětů + 1) * 2

Hodnota heuristické funkce se spočítá jako cena aktuálního stavu sečtená s postihem za porušení tabu seznamu předmětů (nemusí se tak řešit, že není možné udělat další krok, protože jsou všechny tabu). V případě že daný stav je nejlepší dosud nalezený, přičte se hodnota, která zajistí vybrání stavu v dalším kroku (aspirační kritérium, převáží i tabu).

V případě, že se počet kroků začne blížit ke svému limitu, započítává se do heuristické funkce i to, jak jsou prováděné změny neobvyklé (z počtu výskytů předmětů v baťohu z dlouhodobé paměti). V tu chvíli přestane fungovat tabu list na hodnotu heuristické funkce, protože se přestane vracet do předchozí hodnoty (její hodnota je značně ovlivněna předchozími kroky).

Pokud dlouho nedochází k zlepšení nejlepšího nalezeného stavu, skočí prohledávání do stavu získaného z nejlepšího nalezeného odebráním dvou věcí, které strávily nejmenší dobu mimo batoh.

Tabu list občas ignoruje jednu položku (když se má přetočit kruhová fronta, ignoruje se nultá položka).

Prohledávání začíná od prázdného batohu.

Pozorování

Prohledávání vždy na testovaných instancích našlo globální minimum, své pozorování jsem tedy soustředil na to, jak dlouho trvá, než ho dosáhne.

Závislost relativní chyby na počtu kroků

První graf zachycuje vývoj relativní chyby na počtu kroků. Jsou zobrazeny jen 4 instance (2 konvergujíví rychle a 2 pomalu), ale průběh u ostatních je velmi podobný.

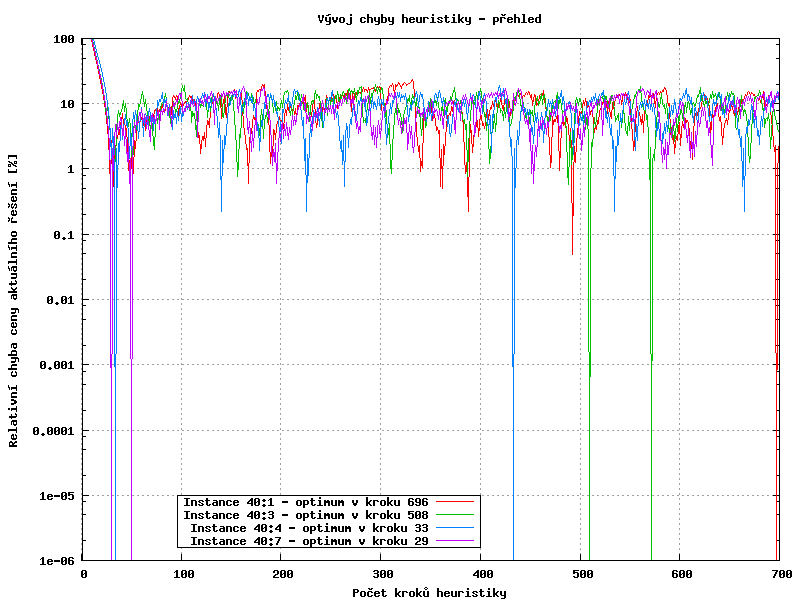
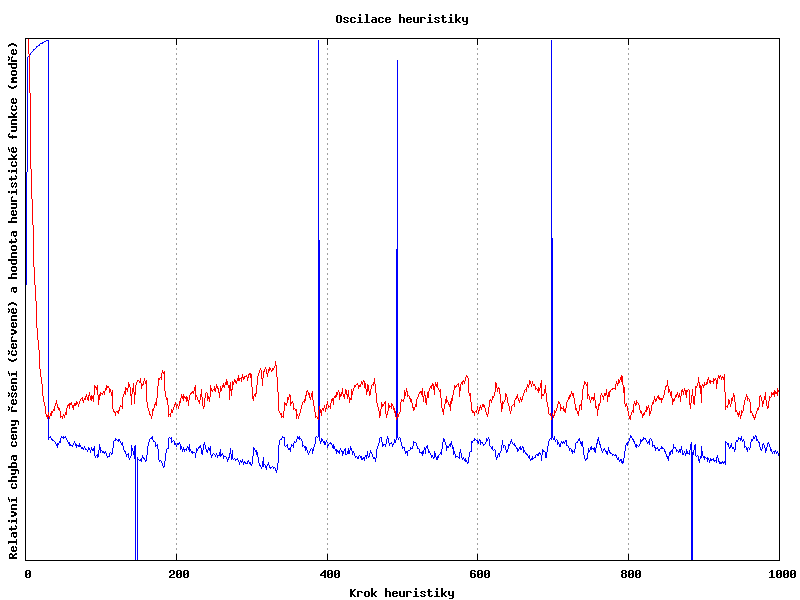
Podívejme se ještě blížeji na vývoj chyby první instance a na hodnotu heuristické funkce v přislušných krocích.

Dobře je vidět, jak se zpočátku vždy najde lepší řešení - heuristická funkce ve všech krocích obsahuje "bonus" za nalezení lepšího řešení a relativní chyba klesá.

Poté přestanou být nalezená řešení lepší a hodnota heuristiky spadne. Prohledává se dál, důležité je, že průběh heuristické funkce není periodícký a hledání se nemotá v kruzích.

Zhruba u kroku 150 je vidět pokles heuristiky z důvodu porušení tabu listu.

V blízkosti kroku 390 je vidět nalezení zlepšujícího tahu do lokálního minima.

A v kroku 696 je objeveno optimální řešení.

Osy Y grafu je logaritmická a průběhy nejsou ve stejném měřítku.

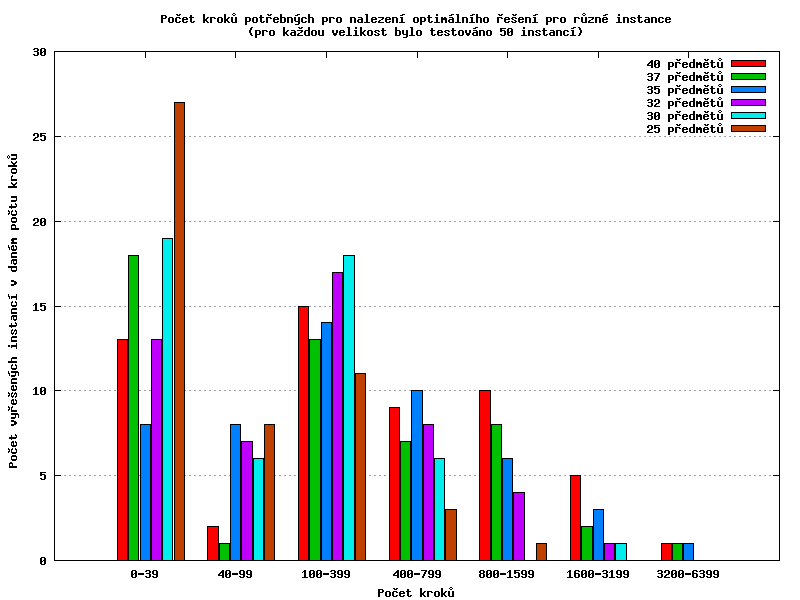
Následuje histogram zobrazující počet instancí (osa Y) dané velikosti (barva sloupce), které dosáhly optima na počet kroků (osa X). Z grafu je vidět, že pokud počet kroků zvolíme roven druhé mocnině počtu předmětů, téměř vždy najdeme optimální řešení.

Závěr

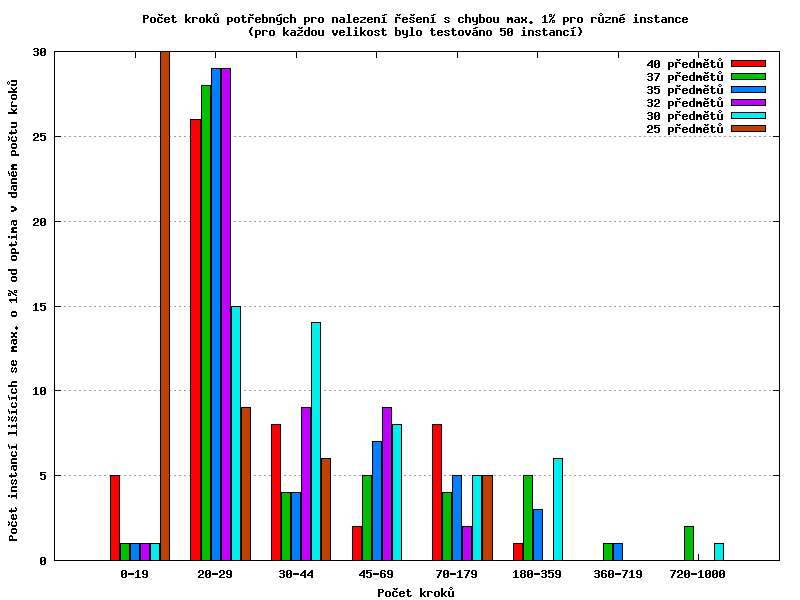
Testoval jsem více různých algoritmů (jiné druhy restaru, další tabu listy...) a několik způsobů výpočtů heuristické funkce a překvapilo mě, že se mi nakonec podařilo najít kombinaci, která na testovaných instancích nikdy neuvázla v lokálním minimu a vždy se dostala až do minima globálního.

Největší problém pri použití tabu prohledávání je jeho spojení s heuristikou tak, aby s tabu seznamy nepůsobily proti sobě. Například při použití tabu seznamu na hodnotu heuristiky a závislostí heuristiky na odchylce od průměrné hodnoty heuristiky, jsem dostal horší výsledky než když se tyto způsoby použily každý zvlášť.