Experimentální hodnocení algoritmů řešící problém batohu

Úvod

Pro řešení problému batohu existuje mnoho algoritmů jak exaktních, tak přibližných. O jejich vlastnostech toho není mnoho známo, pouze pro kombinované heuristiky byla dokázána maximální chyba. Chceme-li vědět více, musíme vyhodnocovat experimentálně.

Budeme sledovat dva podstatné parametry - kvalitu řešení a výpočetní náročnost. Uvedeme-li obě tyto veličiny do vytahu, dozvíme se, pro které kombinace nároků na čas a kvalitu je ten který algoritmus nejvýhodnější.

Kvalita řešení

Pro instance, kde známe exaktní řešení, se kvalita dá měřit absolutně. Tam, kde srovnáváme heuristiky mezi sebou, můžeme srovnávat pouze relativně. Tyto dva způsoby hodnocení je potřeba rozlišovat a konzistentně mezi nimi volit.

Výpočetní náročnost

Výpočetní náročnost se měří ještě hůře. Celkový čas výpočtu zahrnuje všechny vlivy, selhává však při porovnání výsledků z různých strojů. Zahrnuje také vlivy, které nejsou důležité - například způsob implementace datových struktur. Proto jako měřítko výpočetní složitosti volíme počet testovaných stavů. Poněvadž celkové počty stavů instancí lze snadno odvodit, máme měřítko účinnosti dané výpočetní metody.

Zadání

• Prozkoumejte citlivost metod řešení problému batohu na parametry instancí generovaných generátorem náhodných instancí. Máte-li podezření na další závislosti, modifikujte zdrojový tvar generátoru.
• Na základě zjištění navrhněte a proveďte experimentální vyhodnocení kvality řešení a výpočetní náročnosti. Pokud možno, prezentujte algoritmy jako body v ploše, jejíž souřadnice jsou výše uvedená kritéria.

Pozorování - exaktní algoritmy

Závislost na poměru nosnosti batohu a celkové váhy věcí

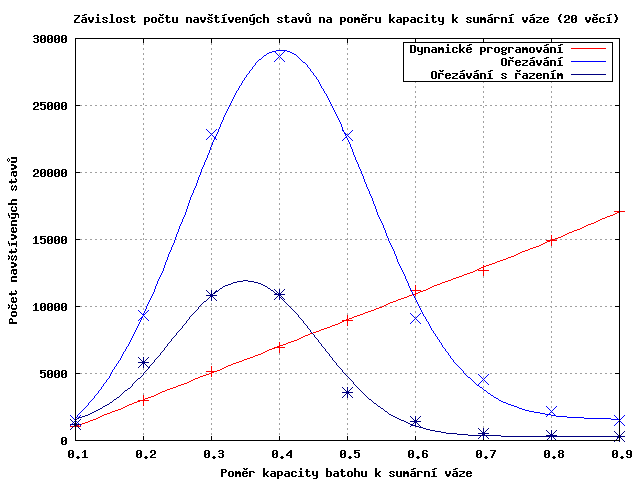
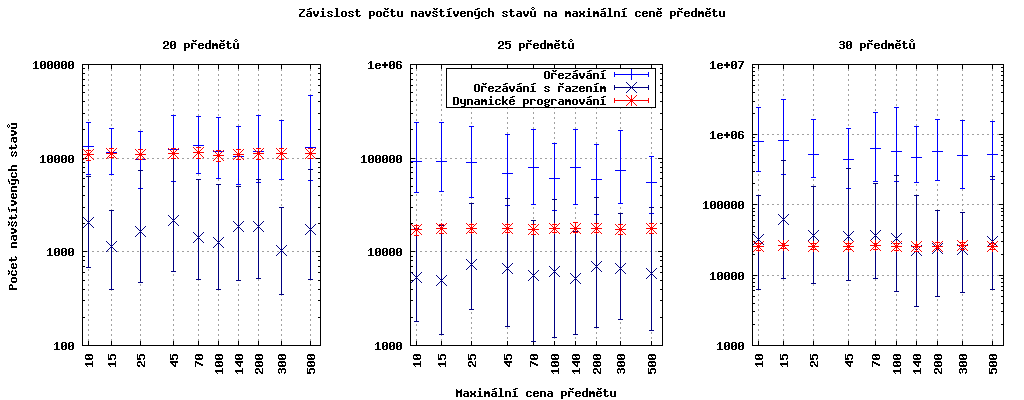
Na prvním grafu pro instance o dvaceti předmětech můžeme pozorovat lineární závislost algoritmu dynamického programování na kapacitě batohu.

Dále je vidět fázový přechod ořezávacích algoritmů od ořezávání spíše podle hmotnosti k ořezávání spíše podle ceny. Při tomto přechodu počet prohledávaných stavů prudce naroste.

Ještě bych upozornil na to, že i když řešení pomocí dynamického programování prohledává více stavů, tak bude pro instance o této velikosti rychlejší, protože na zpracování jednoho stavu potřebuje méně operací.

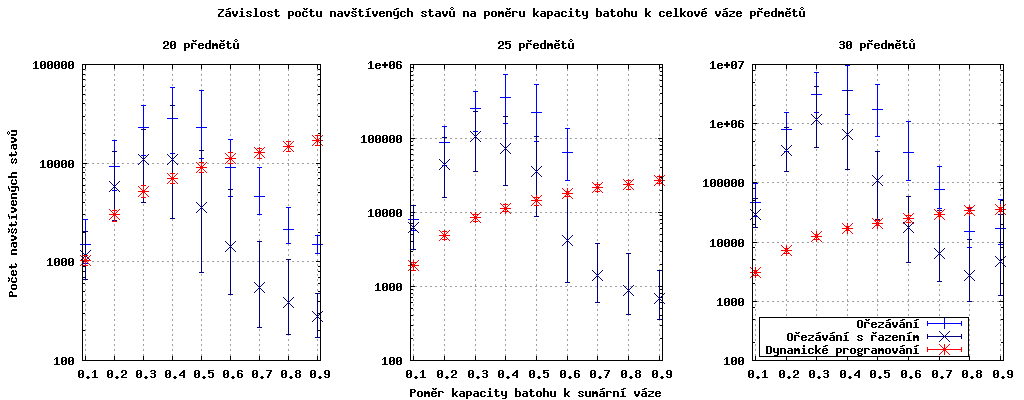
Na následujících grafech je navíc zobrazena směrodatná odchylka a osa y má logaritmické měřítko.

Můžeme pozorovat vyrovnaný počet prohledávaných stavů pro jednotlivé instance u aloritmu řešící problém pomocí dynamického programování.

Dále je vidět, že fázový přechod při zvětšování instancí (přidávání předmětů) nemění svojí "polohu" a rostoucí odchylka počtu prohledaných stavů pro jednotlivé instance.

Závislost na maximální hmotnosti

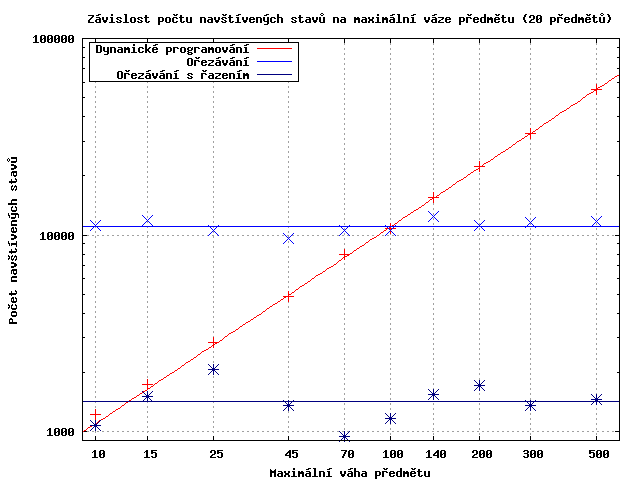
Z průběhu je vidět lineární závislost počtu prohledávaných stavů dynamického algoritmu na maximální váze předmětu. Tato závislost je očekávaná, protože počet prohledávaných stavů dynamického algoritmu lineárně zavisí na kapacitě batohu, která je určena součinem konstanty (zde 0,6) a součtu hmotností všech předmětů.

Ořezávací algoritmy na maximální hmotnosti závislé nejsou.

Ještě bych upozornil na logaritmické měřítko na obou osách.

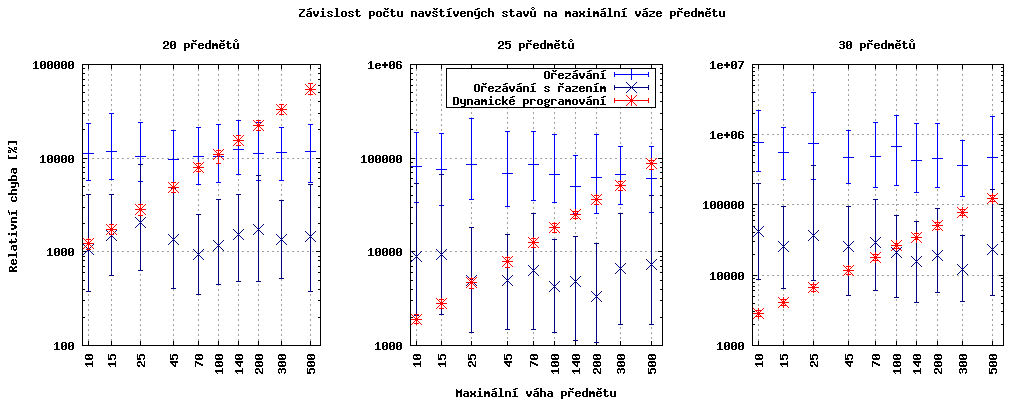
Na grafech se směrodatnou odchylkou si můžeme potvrdit nezávislost počtu prohledávaných stavů ořezávacími algoritmy na maximální hmotnosti předmětu - rozdíly mezi jednotlivými hmotnostmi jsou vždy menší než směrodatná odchylka.

Také si můžeme všimnout, že rozdělení u ořezávacích algoritmů je vychýlené vpravo, kdežto u dynamického algoritmu je spíše symetrické.

Závislost na maximální ceně

Ani u jednoho ze zkoumaných exaktních algoritmů se neprokázala závislost počtu navštívených stavů na maximální ceně předmětu. Rozdíly počtu prohledávaných stavů pro různé ceny jsou vždy menší než směrodatné odchylky.

Závislost na granularitě

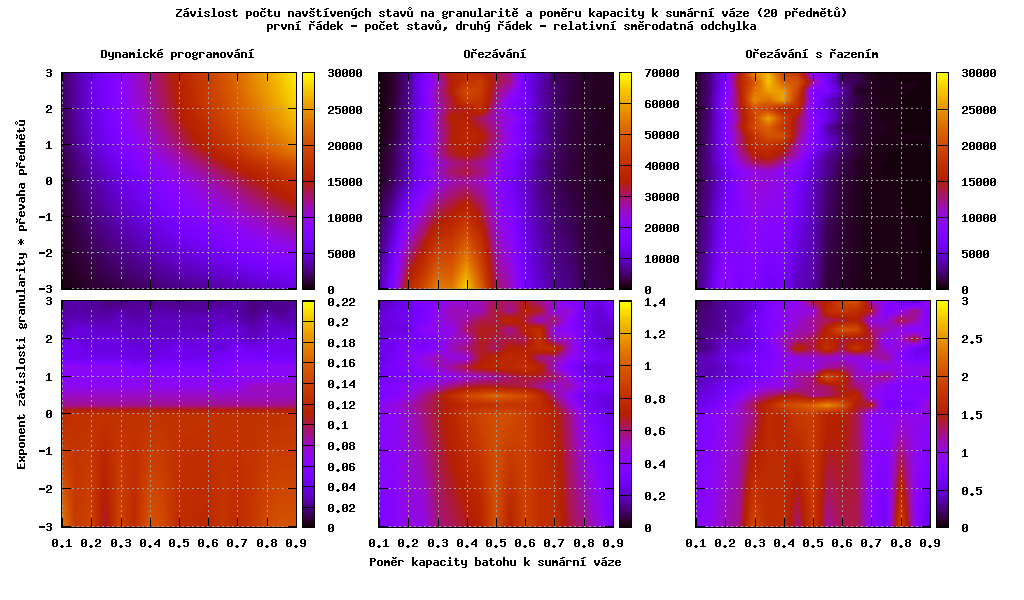
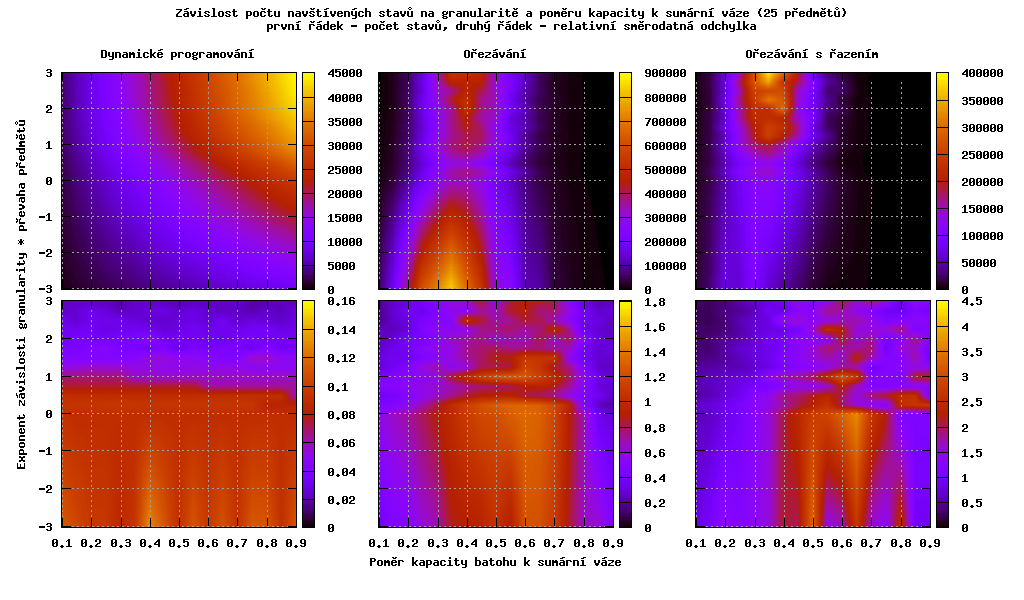
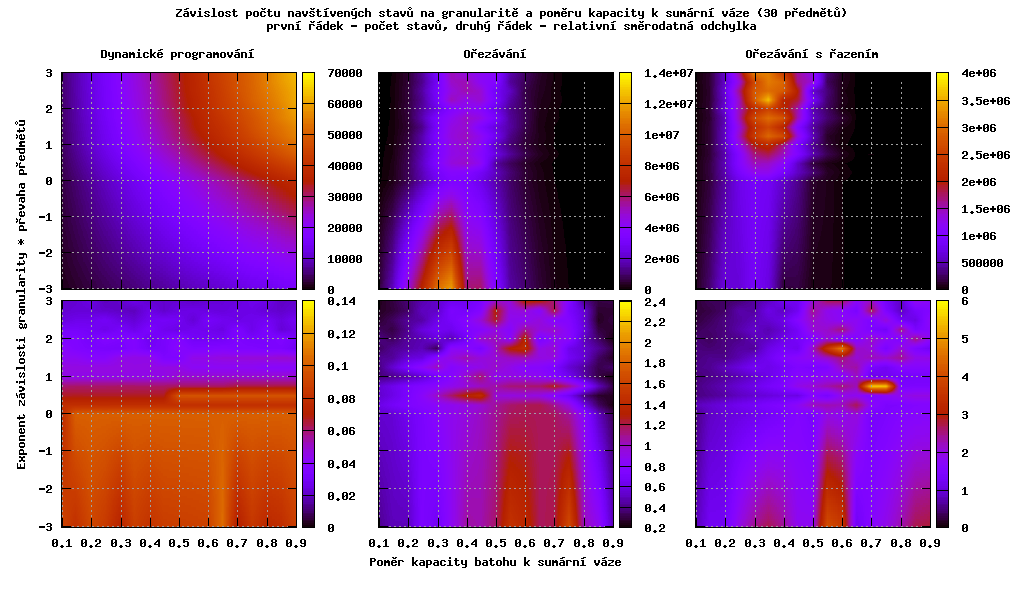
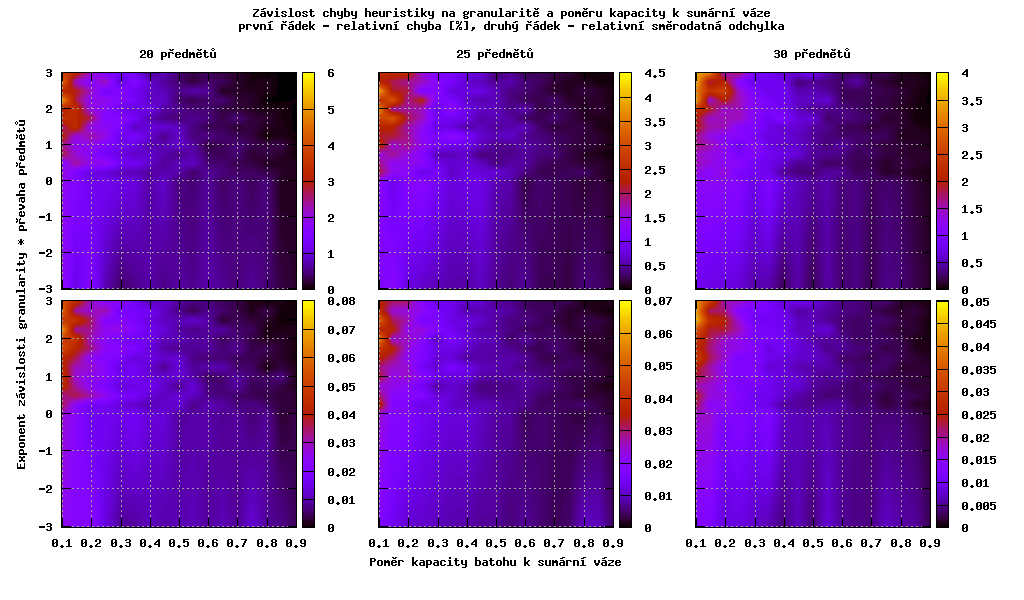
Na následujících grafech je zobrazena závislost počtu prohledávaných stavů na granularitě a poměru kapacity batohu k sumární váze.

Hodnota na ose y vyjadřuje pravděpodobnost přijmutí předmětu do batohu takto

• pro y < 0 platí p = w^y
• pro y >= 0 platí p = (w_max-w)^-y

Můžeme pozorovat, že při převaze malých věcí odstraní řazení u ořezávacího algoritmu fázový přechod, který je tím větší, čím víc jeden druh věcí převažuje.

Dále je vidět závislost počtu prohledávaných stavů algoritmem dynamického programování na převaze věcí a poměru kapacity k sumární váze - obě tyto hodnoty přímo určují kapacitu batohu, na které je algoritmus lineárně závislý. Také pozorujeme, že s převahou velkých věcí klesá rozptyl počtu prohledávaných stavů.

Pozorování - heuristiky

Závislost na poměru nosnosti batohu a celkové váhy věcí

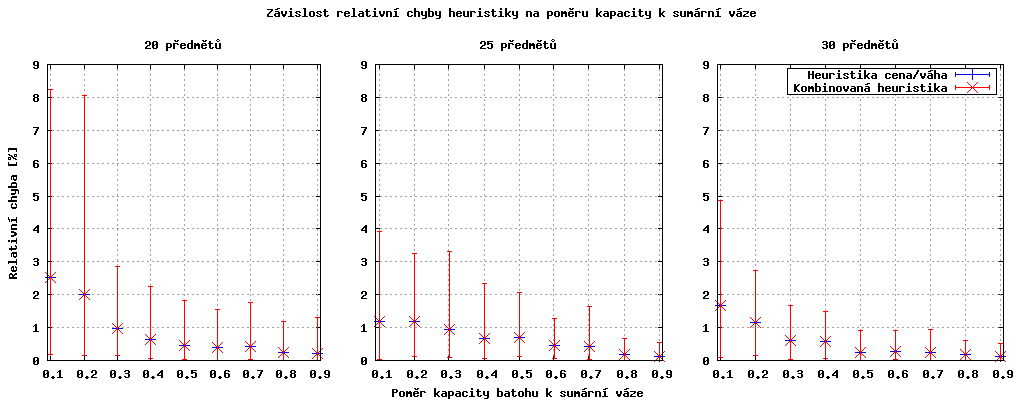
Heuristika dává lepší výsledek s rostoucím poměrem nosnosti batohu a celkové váhy předmětů. Je to způsobeno tím, že čím více předmětů se do batohu vejde, tím méně se projeví špatný výběr některého z nich.

Závislost na maximální hmotnosti

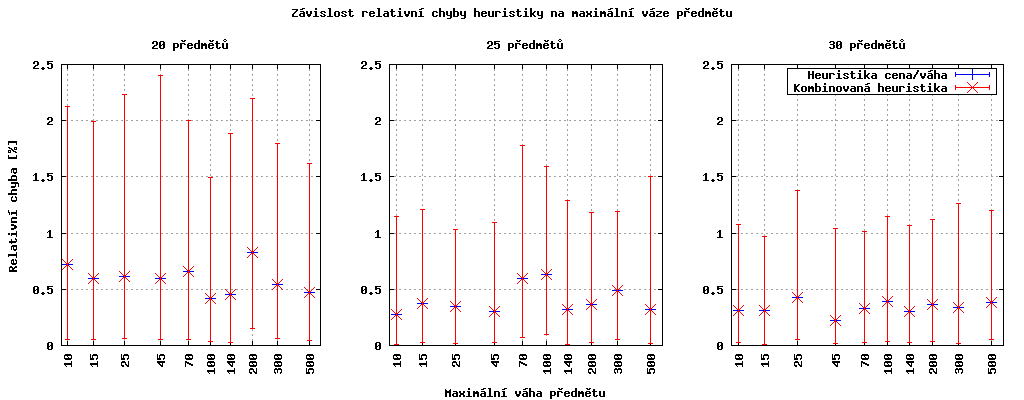
V tomto případě se žádná závislost neprokázala, rozdíly chyb u jednotlivých hmotností jsou mnohem menší než směrodatné odchylky.

Závislost na maximální ceně

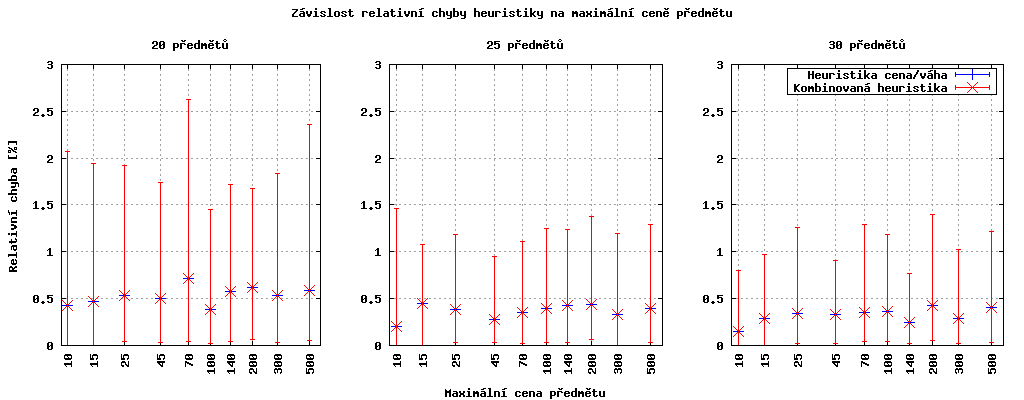
Stejně jako v předchozím případě se zde žádná závislost neprokázala, rozdíly chyb u jednotlivých cen jsou znatelně menší než směrodatné odchylky.

Závislost na granularitě

Na následujícím grafu můžeme pozorovat zhoršující se výsledek heuristiky při zvyšování výskytu velkých věcí a zmenšující se kapacitě batohu. Naopak nejlepší výsledky dostáváme pro velkou kapacitu batohu a těžké předměty.

Výsledky byly opět stejné pro obě heuristiky, proto je zobrazen jen jeden graf.

Závěr

Na závěr shrnu závislosti algoritmů na jednotlivých parametrech instance. U heuristiky se uvažuje přesnost, u exaktních algoritmů počet navštívených stavů.