Petr Malát	Úloha 1	Úloha 2	Úloha 3	Úloha 4	Úloha 5	Úloha 6	Pondělí 11:00

Řešení problému batohu

Popis problému

K dispozici jsou dva kýble (předem daných obecně rozdílných objemů), vodovodní kohoutek a kanál. Na počátku jsou oba kýble prázdné. Vaším úkolem je docílit toho, aby v jednom kýblu byla voda o předem stanoveném objemu, přičemž můžete pouze naplnit plný kýbl z kohoutku, vylít celý kýbl do kanálu a přelít jeden kýbl do druhého tak, aby druhý kýbl nepřetekl. Problém lze zobecnit tím, že připustíme užití většího počtu kýblů, aby na počátku řešení byla v kýblech nějaká voda, a že předepíšeme koncový objem vody v každém kýblu.

Zadání

Naprogramujte řešení 0/1 problému batohu metodou větví a hranic (B&B) tak, aby omezujícím faktorem byla hodnota optimalizačního kritéria. Tj. použijte ořezávání shora (překročení kapacity batohu) i zdola (stávající řešení nemůže být lepší než nejlepší dosud nalezené)
Naprogramujte řešení 0/1 problému batohu nebo alespoň 0/1 exaktního problému batohu bez cen metodou dynamického programování.
Naprogramujte řešení 0/1 problému batohu heuristikou podle poměru cena/hmotnost s testem nejcennější věci.

Řešení

Algoritmy jsou naprogramované v jazyce C a měření proběhlo na počítači s CPU PentiumIII @ 700MHz.

Hrubá síla

Použil jsem program z první úlohy, který rekurzivním algoritmem prochází všechny možnosti, které nepřetíží batoh. Zdrojový kód je zde.

Metoda větví a hranic

Vyšel jsem z programu řešícího problém hrubou silou a doplnil test, zda se může přidáním dalších věcí dosáhnout lepšího výsledku, než jaký byl dosud nalezen - před spuštěním rekurzivního algoritmu se vypočíta pro každou věc V_i součet cen věcí V_j: j>i. Poté se při procházení kontroluje, zda stávajicí cena + cena všech věcí, které se budou ještě přidávat do batohu, není horší než dosud nejlepší nalezené řešení - v tom případě se dále z tohoto uzlu už neprohledává.
Zdrojový kód je zde.

Metoda větví a hranic s řazením (Řaď a ořež)

Protože metoda větví a hranic má problémy pro určitá pořadí věcí (například když je poslední těžká a drahá věc), upravil jsem ještě algoritmus tak, že před vlastním řešením nejdříve seřadí věci podle hmotnosti (testoval jsem i řazení podle ceny a podle poměru cena/váha, ale hmotnost vycházela nejlépe). Takto modifikace algoritmus zrychlila více, než přidání ořezávání podle ceny. Zdrojový kód je zde.

Dynamické programování

Algoritmus si na začátku vytvoří vynulované pole o délce o jedna vyšší, než je kapacita batohu. Každá položka pole obsahuje cenu (nejlepší cena, kterou je možné dosáhnout s danou kapacitou) a stav věcí (které věci jsou v batohu). Potom pro každou věc projde pole od nejvyššího prvku až po prvek na místě odpovídající zpracovávané věci a zkouší, zda cena zpracovávané věci a cena na pozici o hmotnost nižší je lepší. Pokud ano upraví aktuální pozici.
Pro k-tou věc je prvek pole na pozici m nejlepší řešení batohu o kapacitě m pro prvních k věcí. Zdrojový kód je zde.

Heuristika cena/váha a kombinovaná heuristika

Kombinovaná heuristika rozšiřuje původní heuristiku podle poměru cena/váha o test, zda řešení sestávající z nejcennější věci, která se vejde do batohu, není lepší. Zdrojový kód jednoduché heuristiky je zde a kombinované zde.

Pozorování

Srovnání výpočetních časů hrubé síly, B&B a dynamického programování

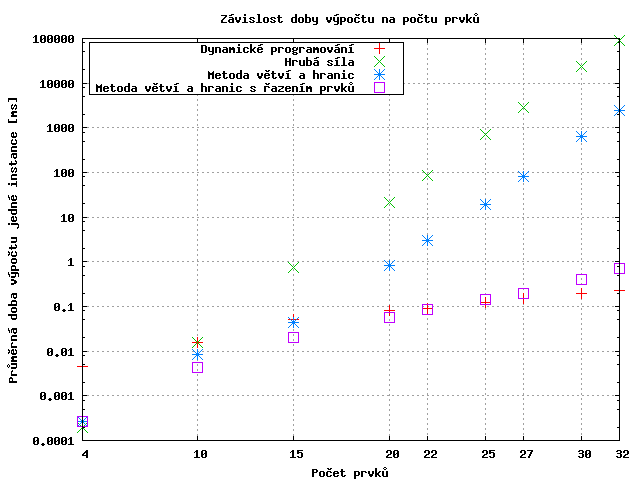
Z naměřených hodnot je velmi dobře patrný exponenciální vzestup doby výpočtu hrubé síly a B&B, které je asi o řád rychlejší než hrubá síla, ale objevovaly se i instance, kde se ořezávání podle cen vůbec neuplatnilo a B&B a hrubá síla tak měly stejnou dobu výpočtu.
Velké zlepšení bylo přidání řazení k B&B - potom není problém řešit i instance o větší velikosti (pro 40 věcí výpočet jedné instance trval v průmeru 7 ms).
Jasně nejrychlejší pro větší instance bylo řešení s využitím dynamického programování (pro 40 věcí se řešila jedna v průměru instanci 0.5 ms).

N	Průměrná doba řešení jedné instance [ms]
N	Dynam. prog.		Řaď a ořež		Hrubá síla		Met. větví a hranic
4	0	,00461	0	,00026	0	,00020	0	,00027
10	0	,01560	0	,00441	0	,01602	0	,00839
15	0	,05074	0	,02010	0	,73960	0	,04414
20	0	,08186	0	,05592	21	,738	0	,82968
22	0	,08814	0	,08401	85	,675	2	,9953
25	0	,12240	0	,14185	701	,55	19	,518
27	0	,15304	0	,19156	2853	,3	80	,881
30	0	,19340	0	,39656	23405		628	,13
32	0	,23177	0	,72253	91973		2483	,4

Srovnání vylepšené heuristiky s původní

Je jasné, že kombinovaná heuristika nemůže být horší než heuristika cena/váha, nicméně její hlavní výhoda - jistota, že její řešení bude maximálně o polovinu horší než optimální - se zde neprojevila, protože ani jednoduchá heuristika se na testovaných instancích nedopustila takové chyby.
Protože doba výpočtu pomocí kombinované a jednoduché heuristiky je téměř stejná (mají stejnou asymptotickou složitost), je kombinovaná heuristika lepší díky nižší průměrné chybě a pevným omezením maximalní odchylky od nejlepšího řešení.

N	Relativní chyba [%]
	cena/váha		kombinovaná
	průměrná	maximální	průměrná	maximální
4	2.174	36.363	1.328	24.745
10	1.286	11.480	1.104	11.480
15	0.475	8.542	0.305	2.774
20	0.600	8.433	0.431	4.079
22	0.686	7.228	0.542	3.017
25	0.498	3.678	0.424	2.587
27	0.501	10.601	0.289	1.845
30	0.507	5.513	0.397	1.749
32	0.341	3.340	0.274	2.278

Závěr

Rychlostním vítězem dávajícím optimální řešení se stal algoritmus využívající dynamického programování, který má pseudopolynomiální složitost. Problém by byl, kdyby ceny věcí nebyla celá čísla - pak by se počet různých možných hmotností zvýšil a vyplatilo by se uvažovat o nasazení B&B s řazením.

Kombinovaná heuristika dává v průměru lepší řešení a protože rozdíl v době potřebné na výpočet je zanedbatelný, je tak lepším kandidátem pro nasazení. Další výhodou je záruka maximální odchylky od optimálního řešení.