Petr Malát	Úloha 1	Úloha 2	Úloha 3	Úloha 4	Úloha 5	Úloha 6	Pondělí 11:00

Řešení problému batohu

0/1 problém batohu

Je dáno

celé číslo n (počet věcí)
celé číslo M (kapacita batohu)
konečná množina V={v₁, v₂, ..., v_n} (hmotnosti věcí)
konečná množina C={c₁, c₂, ..., c_n} (ceny věcí)

Zkonstruujte množinu X={x₁, x₂, ..., x_n}, kde každé x_i je 0 nebo 1, tak, aby platilo
v₁x₁ + v₂x₂ + ... + v_nx_n <= M (batoh nebyl přetížen) a výraz c₁x₁ + c₂x₂ + ... + c_nx_n nabýval maximální hodnoty pro všechny takové množiny (cena věcí v batohu byla maximální).

Zadání

Naprogramujte řešení 0/1 problému batohu hrubou silou. Na zkušebních datech pozorujte závislost výpočetního času na n. Naprogramujte řešení 0/1 problému batohu heuristikou podle poměru cena/váha.

Pozorujte:

závislost výpočetního času na n. Grafy jsou vítány (i pro exaktní metodu)
průměrné zhoršení proti exaktní metodě
maximální relativní chybu

Řešení

Hrubá síla

Řešení pomocí hrubé síly projde všechny přípustné možnosti a vždy najde nejlepší řešení.

Rekurzivní funkcí se postupně procházejí všechny možné stavy nepřetíženého batohu. Zapamatuje se nejlepší stav a jeho cena. Zdrojový kód programu je zde.

Heuristika podle poměru cena/váha

Řešení heuristikou nemusí najít optimální řešení. Jeho výhoda je v rychlosti.

Předměty se sestupně seřadí (quicksortem) podle poměru cena/váha. Potom se v pořadí vzniklém řazením přidávají do batohu (v případě, že ho nepřetíží). Zdrojový kód programu je zde.

Pozorování

Měření byla provedena na počítači s procesorem Pentium III@700MHz a pod operačním systémem Linux 2.6.22. Programy jsou naprogramovány v jazyce C a byly přeloženy pomocí gcc 4.2.1.

Závislost výpočetního času na n

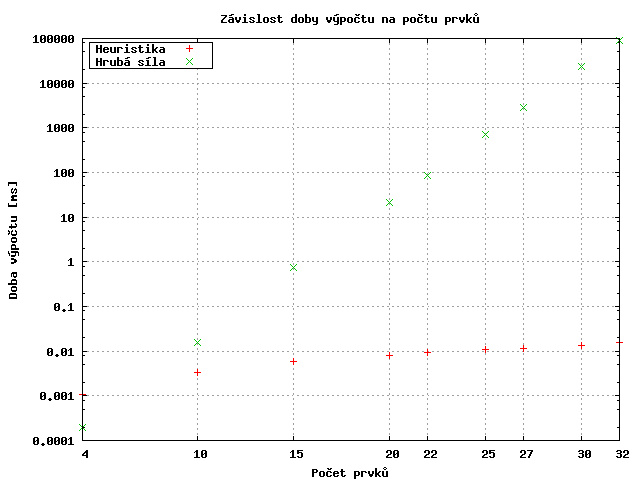
n	Doba výpočtu [ms]
n	hrubá síla		heuristika
4	0,	0002	0,	0011
10	0,	0160	0,	0034
15	0,	7396	0,	0060
20	21,	7375	0,	0082
22	85,	675	0,	0091
25	701,	55	0,	0106
27	2853,	3	0,	0117
30	23405		0,	0137
32	91173		0,	0153

Z grafu je dobře viditelná exponenciální složitost algoritmu využívajícího hrubou sílu a rychle rostoucí rozdíl doby výpočtu obou algoritmů.

Chyba heuristiky

n	Relativní chyba [%]
n	průměrná		maximální
4	2,	174	36,	36
10	1,	286	11,	48
15	0,	475	8,	543
20	0,	600	8,	434
22	0,	687	7,	229
25	0,	498	3,	679
27	0,	501	10,	60
30	0,	507	5,	514
32	0,	341	3,	341

Z naměřených dat je patrné, že chyba se vzrůstajícím počtem věcí klesá. Důvod bude nejspíše ten, že při větším počtu věcí se méně projeví špatný výběr několika z nich.

Závěr

Je zřejmé, že řešení hrubou silou, které má exponenciální složitost O(2ⁿ), je použitelné pouze pro několik desítek věcí. Řešení pomocí heuristiky podle poměru cena/váha má průměrnou složitost O(n*log(n)), což je složitost řazení věcí. Heuristikou je tedy možné řešit zadání s řádově větším počtem věcí, ovšem za cenu, že nemusíme dostat nejlepší řešení.