Problém vážené splnitelnosti booleovské formule

1. Úvod

1.1 Specifikace problému

Je dána booleovská formule F proměnnných X=(x₁, x₂, ... , x_n) v konjunktivní normální formě. Dále jsou dány celočíselné kladné váhy W=(w₁, w₂, ... , w_n). Najděte ohodnocení Y=(y₁, y₂, ... , y_n) proměnných x₁, x₂, ... , x_n tak, aby F(Y)=1 a součet vah proměnných, které jsou ohodnoceny jedničkou, byl maximální.

1.2 Použité instance

Při práci jsem využill instance ze SATLIBu. Při návrhu algoritmu jsem používal hlavně instance s řízeným počtem implikovaných proměnných, protože počet implikovaných proměnných významně ovlivňuje opbtížnost a je dobré ho znát. Naopak stanovení parametrů a testování jsem prováděl s mixem instancí, protože při řešení praktických problémů počet implikovaných proměnných většinou neznáme.

Instance s vahami jsem získal z předchozích doplněním náhodně vygenerovaných vah.

2. Popis konstrukce algoritmu

V této části popíšu základní algoritmus, který budu postupně po krocích rozšiřovat. U každého kroku se pokusím popsat problémy algoritmu a v dalším kroku je odstranit.

Když se porovnávají ohodnocení (=stavy při prohledávání), tak je větší ten, který má více splněných formulí. V případě rovnosti rozhoduje váha.

Testování provádím na obtížněji řešitelných (v blízkosti fázového přechodu) instancích, protože ty lehké řešil bezproblémů i základní algoritmus.

2.1 Základní algoritmus

Z tohoto algoritmu vycházím, je to nejjednodušší možná implementace tabu-prohledávání. Algoritmus po stanovený počet kroků prohledává stavový prostor, kdy v každém kroku vybere souseda tak, aby došlo k největšímu zlepšení. Množina sousedů jsou ohodnocení proměnných, která se od aktuálního ohodnocení liší maximálně v ohodnocení jedné proměnné. Porovnávání sousedů je na diagramu zvýrazněno zelenou plochou.

Výběr je ještě omezen tabulistem, kdy není možné vybrat souseda, který se liší v proměnné uvedené na tabulistu. Toto omezení je možné porušit v případě splnění aspiračního kritéria - nalezený stav je nejlepší z dosud nalezených (na diagramu označeno modrou elipsou).

V tuto chvíli se také v algoritmu objevuje první proměnná, o které nemůžeme apriori říct, jakou by měla mít hodnotu - délka tabulistu. Otestováním na několika instancích jsem stanovil její hodnotu na 0.2*počet proměnných. Podrobnější stanovení provedu později.

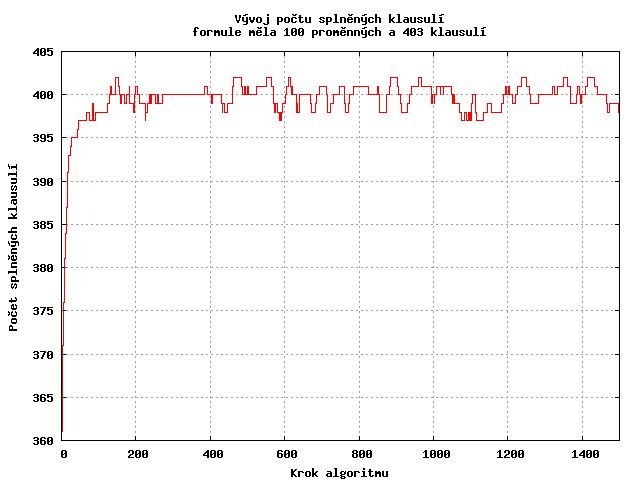
Nyní se podívejme, jak se vyvíjí počet splněných klauzulí v jednotlivých krocích algoritmu. Algoritmus se poměrně rychle dostane k lokálnímu maximu, které se moc neliší od globálního maxima. Poté se ale "neodhodlá" udělat větší krok zpět a pořád bloudí v okolí.

Otestoval jsem zda bloudění je periodické - pro 5 instancí jsem vygeneroval prvních 4000 kroků a sledoval, zda se vybraný vzorek z "konce prohledávání" již někde vyskytuje. Periodičnost se neprokázala.

Odpor algoritmu k přijmutí více zhoršujícího řešení se pokusím vyřešit přidáním dlouhodobé paměti v dalším kroku.

2.2 Pokročilý algoritmus - dlouhodobá paměť

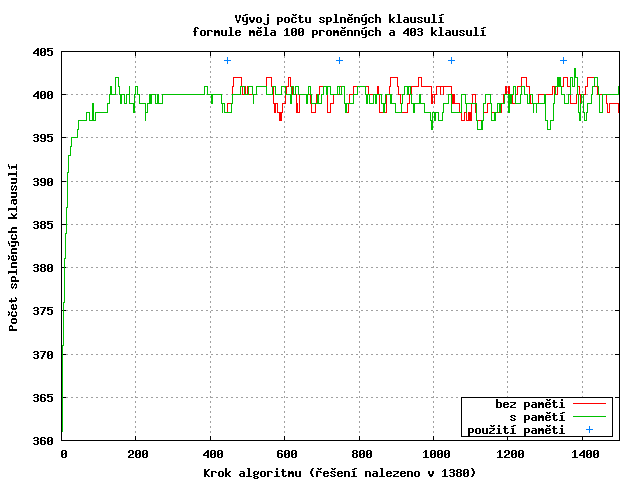
Rozšířím algoritmus o dlouhodobou paměť - bude si pamatovat, kdy naposledy byla každá klausule splněná a kdy naposledy se měnila hodnota proměnné.

V případě, že se po nějakou dobu nebude řešení zlepšovat, algoritmus využije tuto znalost k vynucené negaci nejdéle neměněné proměnné v nejdéle nesplněné klauzuli.

Na grafu pozorujeme, že při vynucené změně ohodnocení proměnné se počet splněných klausulí výrazně nezmění, což je způsobeno částečně tím, že vynucená změna se provede před výběrem nejlepšího souseda, tudíž je zhoršení ihned kompenzováno (provedení opačného kroku zabrání tabulist). Díky tomu algoritmus prohledává více různorodá řešení.

Na demonstračním průběhu je čtvrté použití paměti trefou do černého - řešení je poté nalezeno v několika krocích.

Zavedení paměti vyžaduje i definovat, jak často paměť používat. Pokusem na několika instancích jsem zatím zvolil 3*počet proměnných, přesnější stanovení nechám na závěrečné testování.

Po tomto vylepšení jsem algoritmus nechal řešit 2000 různých instancí (max. počet kroků 10000) a výsledek zobrazil do následujících histogramů.

2.3 Pokročilý algoritmus - restartování

V posledním měření algoritmus buď vždy našel řešení a nebo mu chybělo splnění jedné klauzule. Nabízí se vyzkoušet, jak algoritmus dopadne, když se spustí z náhodného ohodnocení, které bude ale pozměněno tak, že jediná, minule nesplněná klausule, bude splněna "maximálně" - všechny nenegované proměnné klausule budou nastaveny na 1 a negované na 0.

Restartování úspěšně zafungovalo a jak je vidět na histogramech, počet nevyřešených klauzulí značně poklesl.

Na grafech si dále můžeme všimnout, že pokud algoritmus našel řešení hned na první pokus, tak ho často našel na nízký počet kroků. Naproti tomu, když řešení hledal po restartu, tak ho většinou nalezl až po větším počtu kroků.

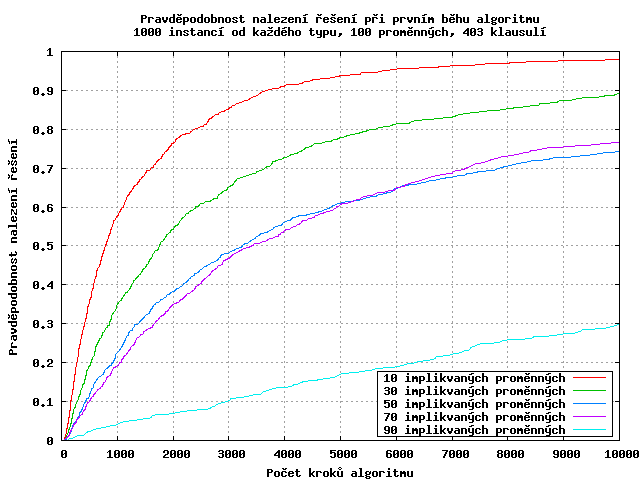
Podívejme se nyní na distribuci pravděpodobnosti nalezení řešení v daném počtu kroků. Závislost má exponencielní tvar, s rostoucím počtem implikovaných proměnných se exponent snižuje.

Abychom optimálně stanovili maximální počet kroků než dojde k restartu algoritmu, potřebovali bychom znát počet implikovaných proměnných (je vidět, že pro 90 implikovaných proměnných se v 10000. kroku ještě vyplatilo pokračovat, protože distribuční funkce rostla relativně rychle). Bohužel tento údaj nemáme většinou k dispozici, takže počet kroků stanovíme pro průměrný případ (malý graf).

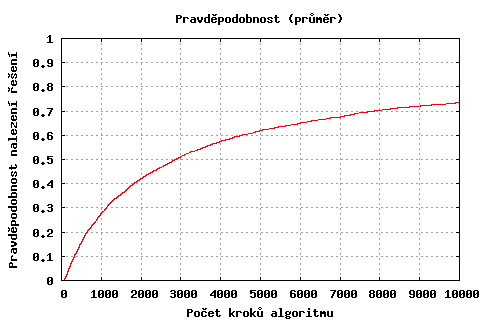
Stanovme prozatím počet kroků na 0.7*počet proměnných² (7000 kroků pro instance na grafech). Až bude celý algoritmus hotový, tak se k němu ještě vrátíme.

Poznámka: Naměřené body vynesené do grafů nejsou nijak prokládány, ale jen pospojovány čarami (které mají většinou nulovou délku, protože bodů bylo víc, než je rastr obrázků).

2.4 Pokročilý algoritmus - randomizace náhodného výběru souseda

U težších zadání (vyšší počet implikovaných proměnných) se stává, že algoritmus po restartu zklouzne zpět do lokálního minima. Pokusím se to odstranit tím, že budu souseda vybírat náhodně.

Z množiny přípustných sousedů s maximálním počtem splněných klauzulí je pravděpodobnost výběru každého z nich přímo úměrná jeho váze.

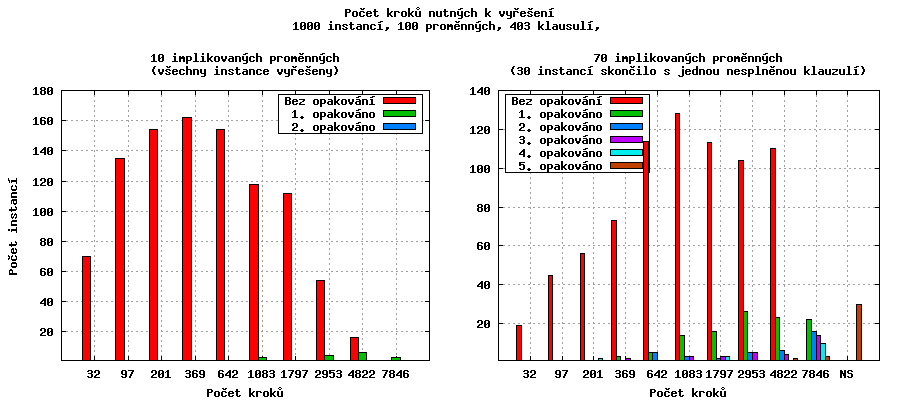
Vliv náhodného výběru jsem posuzoval při jednotkové váze všech předmětů. Změna pro instance o 10 implikovaných proměnných nevypadá moc přesvědčivě, bylo potřeba dokonce o jedno opakování více - tři instance byly vyřešeny až při druhém opakování. Tento rozdíl (3 ze 1000) je ale zanedbatelný. K větším rozdílům docházelo u většího počtu implikovaných proměnných - u 70 se algoritmus zlepšil o 10 (třicet nenalezených řešení místo čtyřiceti) u 90 implikovaných proměnných o 45 (200 nenalezených řešení místo 245).

3. Testování, stanovení parametrů

Parametry budu ladit pro nejtěžší instance, pro které je typické to, že poměr klausulí a proměnných (pro konstantní počet proměnných v klausuli) je konstantní. Mám k tomu dva hlavní důvody:

• U lehkých úloh nezpůsobí horší nastavení parametrů tak zásadí propad ve výkonnosti
• Díky konstantnímu poměru počtu klauzulí a proměnných u těžkých instancí tak odpadne jeden stupeň volnosti

Dále z časových důvodů budu předpokládat nezávislost vlivu jednotlivých parametrů a parametry budu optimalizovat pro klauzule o 3 proměnných (3-SAT), i když algoritmus je napsán obecně a umí pracovat i s větším počtem literálů v klausuli.

3.1 Stanovení optimální délky tabulistu

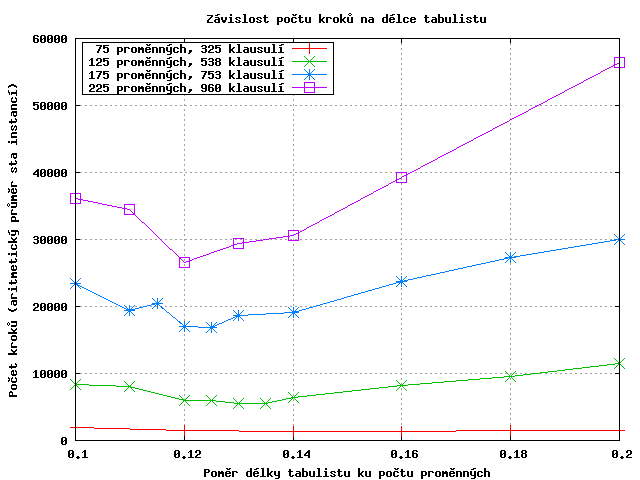
Podle přibližného měření z odstavce 2.1 předpokládám optimální délku tabulistu někde mezi 0.1 a 0.2 násobku počtu proměnných. S krokem 0.02 projdu tento interval a změřím počet kroků pro jednotlivé instance (100 instancí od každého druhu). Dále provedu zpřesňující měření v okolí minimálních hodnot.

Maximální počet kroků byl nastaven na 0.7*počet proměnných², pokud algoritmus nenalezl řešení, byl mu započítán dvojnásobek max. počtu kroků.

Body jednotlivých druhů instancí jsou pro přehlednost pospojovány čarami.

Z dat zobrazených do předchozího grafu vyberu vyberu pro každý počet proměnných délku tabulistu, s kterou algoritmus dosáhl nejmenšího počtu kroků, a body zobrazím do grafu (vpravo). Na první pohled je vidět, že dobrým kandidátem na proložení je přímka. Přímku určím pomocí metody nejmenších čtverců:

3.2 Stanovení, kdy použít dlouhodobou paměť

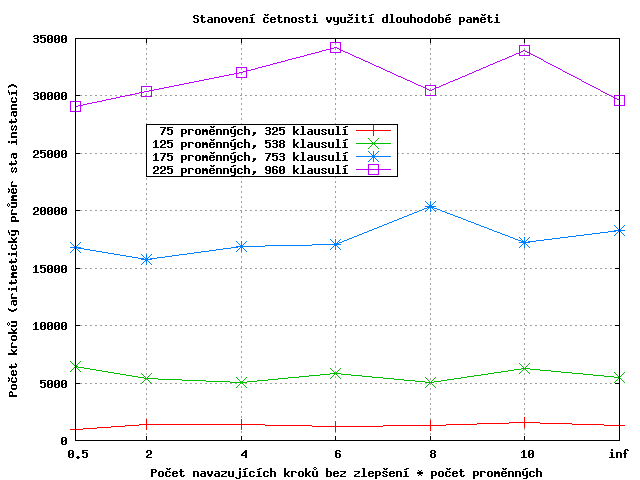
Zde situace není tak jasná jako v předchozím případě, zásah paměti ovlivnuje jen některé instance a proto rozdíly nejsou moc velké. Výkonnost algoritmu by vynecháním tohoto kroku nijak významně nepoklesla, ale protože zde přeci jen malé zlepšení je (hlavně při větším počtu implikovaných proměnných), tak tuto část ponechám.

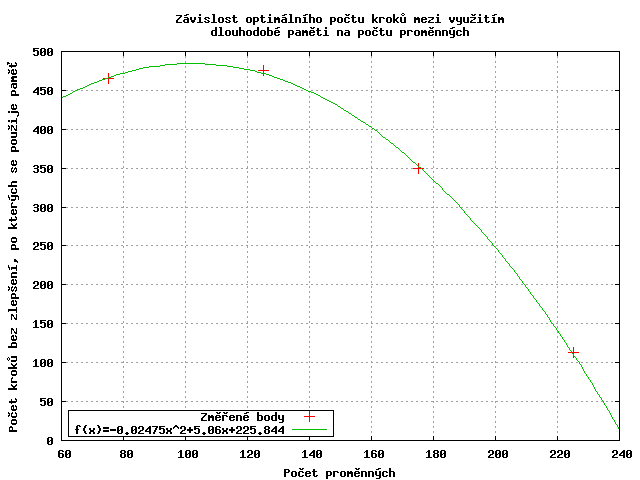
Aproximace získaných bodů pomocí paraboly je sice přesná, ale nebude nejspíše tím, co hledáme - třeba proto, že pro asi 250 proměnných by se dlouhodobá paměť používala v každém nezlepšujícím kroku, což by úplně vyřadilo zbytek algoritmu.

Závislost, pokud vůbec nějaká je, je složitější a pro její určení by bylo potřeba většího počtu bodů. Jako prah pro využití dlouhodobé paměti tedy zvolím bod 2*počet proměnných, který je v součtu přes všechny druhy instancí nejlepší.

3.3 Stanovení počtu kroků do restartu

Počet kroků algoritmu stanovím na základě distribuce pravděpodobnosti nalezení řešení v prvním běhu. Při výběru by se měla zohlednit, jak absolutní hodnota pravděpodobnosti, tak i jak rychle v daném místě roste.

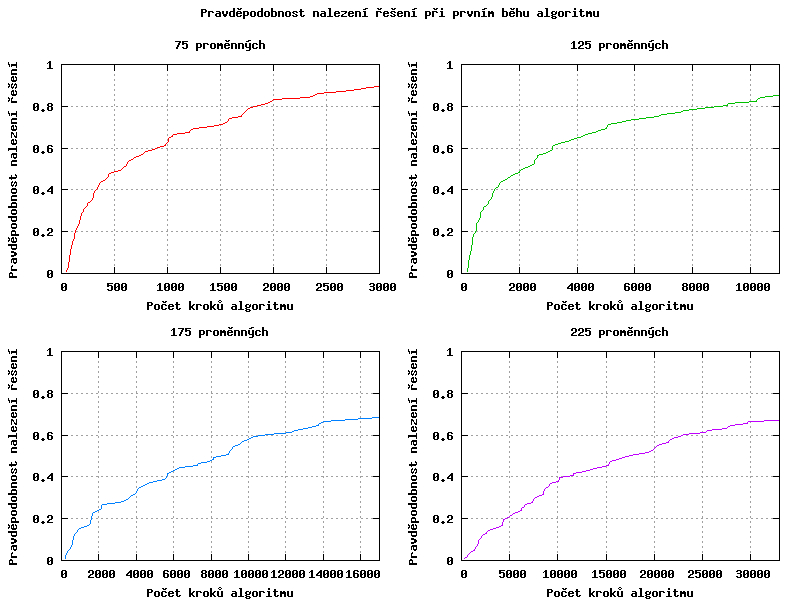
Předchozí graf byl získán za pomoci prvotního nastavení z odstavce 2.3 a protože se nastavení osvědčilo i pro různorodé instance, nebudu ho měnit.

Pro stanovení počtu kroků po restartu využiji také poznatek z odstavce 2.3 - průměrný počet kroků na nalezení řešení je vždy vyšší než při předchozím běhu - a počet kroků při restartu zdvojnásobím.

Celkový počet kroků nastavím vyšší, aby algoritmus měl možnost hledání několikrát zopakovat. Tento parametr také bude jediný, který bude moci uživatel specifikovat a ovlivňovat tak kvalitu řešení na úkor doby výpočtu.

Pro ilustraci ještě uvádím nutný počet kroků pro dosažení zvolené hladiny pravděpodobnosti pro různě velké instance (graf vpravo).

3.4 Otestování výběru cennějších řešeních

Otestování kvality výběru cennějších řešení je složitější v tom, že nevím, jaké je globální maximum a nemůžu tedy přesně říci, jak daleko od něj algoritmus skončí. Testování provedu tedy tak, že budu porovnávat váhu řešení algoritmu, který z váhou nijak nepracuje, a algoritmu, který cennější řešení upřednostňuje.

Spočítám průměrnou váhu ze sta instancí, nevyřešené instance se započítávají za 0. Váhy literálů jsou rovnoměrně vybrány z intervalu <1, počet literálů>

• Bez preference - váhy se při výpočtu nijak neuvažují, získané řešení je průměrně dobré.
• Podle váhy - při porovnání je váha na druhém místě za cenou, při výběru z množiny sousedů se stejným počtem splněných klausulí je pravděpodobnost výběru každého z nich přímo úměrná váze.
• "Kvadratická pravděpodobnost" - jako předchozí, ale pravděpodobnost výběru souseda je místo váhy přímo úměrná druhé mocnině váhy.

Jak je vidět z tabulky, tak přílišná preference souseda s vyšší váhou zhorší průměrnou váhu řešení. Je to způsobeno tím, že se tak sníží náhodnost algoritmu a ten častěji zklouzne do již prozkoumané slepé uličky a nenalezne přípustné řešení (skončí sice s větší sumou vah literálů, ale také s jednou nebo dvěma nesplněnými klausulemi).

4. Implementace

Rozšíření CNF formátu o váhy

Implementace v jazyce C

• Implementace tabulistu: syntaxe, zdroják
• Reprezentace problému: syntaxe, zdroják
• Heuristika (a main): syntaxe, zdroják

5. Závěr

Nejobtížnějším úkolem při návrhu algoritmu je správné určení jednotlivých parametrů. V případě (neznámé) závislosti vlivu jednotlivých parametrů nutný počet testů roste exponenciálně. Musíme tedy při návrhu dobře zvážit, co zanedbat a co naopak nastavit nejpřesněji a dobře zvolit testované instance.

Nejvíce citlivý je algoritmus na nastavení správné délky tabulistu, kdy se při změně poměru délky k počtu literálů o jednu desetinu, zvýší počet kroků na více než dvojnásobek.

Implementovaný algoritmus hodnotím jako zdařilý, samozřejmě by šlo přidat další věci (měnící se délku tabulistu, více věcí v dlouhodobé paměti...) a pak zopakovat testování a ladění parametrů, ale testování je značně výpočetně náročné a algoritmus je už teď schopen úspěšně řešit i těžké instance.